| У одній руці у вас ножиці. У іншій велике кільце, склеєне з довгої паперової стрічки. Ножиці протикають цю стрічку і акуратно розрізають її уподовж - точно посередині. "Ну ось, - подумаєте ви, - зараз вийдуть два окремі кільця. Але що це? Замість двох кілець виходить одне! Причому воно більше і тонше початкового. "Такого не буває", - скажете ви. Буває. І навіть ще й не таке! Якщо тільки в руках у вас не звичайне паперове кільце, а дивовижна
СТРІЧКА МЕБІУСА.
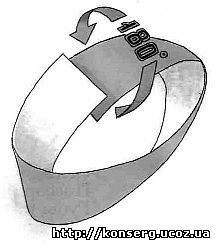 Німецький астроном і математик Август Фердинанд Мебіус узяв одного разу паперову стрічку, повернув один її кінець на пів-оберта (тобто на 180 градусів), а потім склеїв його з іншим кінцем. Чи то від нудьги він це зробив, чи то заради наукового інтересу - тепер уже невідомо. Зате напевно відомо, що саме так і з'явилася ще в позаминулому столітті знаменита стрічка Мебіуса. Німецький астроном і математик Август Фердинанд Мебіус узяв одного разу паперову стрічку, повернув один її кінець на пів-оберта (тобто на 180 градусів), а потім склеїв його з іншим кінцем. Чи то від нудьги він це зробив, чи то заради наукового інтересу - тепер уже невідомо. Зате напевно відомо, що саме так і з'явилася ще в позаминулому столітті знаменита стрічка Мебіуса.
Чим же вона знаменита? А тим, що поверхня стрічки Мебіуса має тільки одну сторону. Це легко перевірити. Візьміть олівець і почніть закрашувати стрічку в якому-небудь напрямі. Незабаром ви повернетеся в те місце, звідки почали. А зараз подивіться уважно: закрашеною виявилася вся стрічка цілком! Адже ви її не перевертали, щоб закрасити з іншого боку. Та і не змогли б перевернути, навіть якщо б дуже захотіли. Тому що поверхня стрічки Мебіуса - одностороння. Ось така у неї цікава властивість.
Що ж з цієї властивості виходить? А виходять дивовижні перетворення стрічки, якщо розрізати її уподовж. Точно посередині - ви вже пробували. А ось якщо розрізати стрічку на відстані третини її ширини від краю, то отримаємо відразу два кільця - одне велике і зчеплене з ним маленьке. Якщо ж розрізати ще і маленьке кільце уподовж посередині, то вас у руках опиниться переплетення двох кілець - однакових за розміром, але разних по ширині. Чудеса?.. Спробуйте самі!
Ну а що, цікаво, вийде, якщо перед склеюванням стрічки перекрутити її двічі (тобто на 360 градусів)? Така поверхня буде вже двосторонньою. І щоб закрасити все кільце цілком, вам доведеться неодмінно перевернути стрічку на іншу сторону.
Проте властивості цієї поверхні не менш дивовижні. Адже якщо розрізати її уподовж посередині, то ви отримаєте два однакові кільця, але знову ж таки зчеплених між собою. А розрізавши кожне з них ще раз уподовж посередині, ви виявите вже чотири кільця, сполучених один з одним. Можна тепер рвати ці кільця по черзі - і ті, що залишаться будуть як і раніше зчеплені разом.
Неважко здогадатися, про що ви зараз задумалися; а що вийде, якщо стрічку перекрутити на три обороти і склеїти.
Що ж, ваша цікавість виправдана. І у вас є чудова можливість задовольнити її самостійно! Але при цьому непогано було б скористатися такими радами:
1. Узяти не паперову стрічку, а смужку будь-якої тканини.
2. Протягнути її крізь металеве кільце.
3. Повернути один з кінців смужки на 3 обороти, тобто на 540 градусів.
4. Зшити обидва кінці.
Тепер можна узяти ножиці і акуратно розрізати кільце з матерії уподовж посередині.
Ножиці краще брати невеликі.
Цікаво було б дізнатися, що у вас вийде в результаті цього експерименту?
Можна, звичайно, провести ще немало дослідів з перекрученням стрічки на чотири обороти, на п'ять, на шість і з подальшим розрізанням кільця уподовж посередині, і на відстані третини від ширини із краю, і т.д.... Але ускладнення експерименту часто не приводить до ефектніших результатів. Недаремно мовиться: "все геніальне просте ". Мабуть, вірно і зворотне твердження: "геніально, як все просте".
І дійсно: проста смужка паперу, але перекручена усього лише раз і склеєна потім в кільце, відразу ж перетворюється на загадкову стрічку Мебіуса і набуває дивовижних властивостей. Такі властивості поверхонь і просторів вивчає спеціальний розділ математики - ТОПОЛОГІЯ.
Наука ця настільки складна, що її в школі не проходять. Тільки у інститутах (і то не у всіх!). Але хто знає, раптом ви станете з часом знаменитим топологом і зробите не одне чудове відкриття. І тоді якусь хитромудру поверхню назвуть вашим ім'ям. Не забудьте тільки тоді всім сказати де саме ви дізналися про цю цікаву властивість стрічки Мебіуса.
|

